小学数学行程知识点
行程问题是小学数学考试的四大题型之一(计算、数论、几何、行程)。今天就带大家一起学习一下如何解决这一类问题!
一般相遇追及问题
包括一人或者二人时(同时、异时)、地(同地、异地)、向(同向、相向)的时间和距离等条件混合出现的行程问题。
建议熟练应用标准解法,即s=v×t结合标准线段画图(基本功)解答。由于只用到相遇追及的基本公式即可解决,在解题的时候,一旦出现比较多的情况变化时,结合自己画出的图分段去分析情况。
复杂相遇追及问题
1
多人相遇追及问题
比一般相遇追及问题多了一个运动对象,即一般我们能碰到的是三人相遇追及问题。解题思路完全一样,只是相对复杂点,关键是标准画图的能力能否清楚表明三者的运动状态。
2
多次相遇追及问题
即两个人在一段路程中同时同地或者同时异地反复相遇和追及,俗称“反复折腾型问题”。
分为标准型(如已知两地距离和两者速度,求n次相遇或者追及点距特定地点的距离或者在规定时间内的相遇或追及次数)和纯周期问题(少见,如已知两者速度,求一个周期后,即两者都回到初始点时相遇、追及的次数)。
标准型解法固定,不能从路程入手,将会很繁,最好一开始就用求单位相遇、追及时间的方法,再求距离和次数就容易得多。如果用折线示意图只能大概有个感性认识,无法具体得出答案,除非是非考试时间仔细画标准尺寸图。
一般用到的时间公式是(只列举甲、乙从两端同时出发的情况,从同一端出发的情况少见,所以不赘述):
单程相遇时间:t单程相遇=s/(v甲+v乙)
单程追及时间:t单程追及=s/(v甲-v乙)
第n次相遇时间:tn= t单程相遇×(2n-1)
第m次追及时间:tm= t单程追及×(2m-1)
限定时间内的相遇次数:N相遇次数=[ (tn+ t单程相遇)/2 t单程相遇]
限定时间内的追及次数:M追及次数=[ (tm+ t单程追及)/2 t单程追及]
之后再选取甲或者乙来研究有关路程的关系,其中涉及到周期问题需要注意,不要把运动方向搞错了。
简单例题:
甲、乙两车同时从A地出发,在相距300千米的A、B两地之间不断往返行驶,已知甲车的速度是每小时30千米,乙车的速度是每小时20千米。
问:
(1)第二次迎面相遇后又经过多长时间甲、乙追及相遇?
(2)相遇时距离中点多少千米?
(3)50小时内,甲乙两车共迎面相遇多少次?
火车问题
特点无非是涉及到车长,相对容易。小题型分为:
1、火车过桥(隧道):一个有长度、有速度,一个有长度、但没速度
解法:火车车长+桥(隧道)长度(总路程) =火车速度×通过的时间;
2、火车+树(电线杆):一个有长度、有速度,一个没长度、没速度
解法:火车车长(总路程)=火车速度×通过时间;
3、火车+人:一个有长度、有速度,一个没长度、但有速度
(1)火车+迎面行走的人:相当于相遇问题
解法:火车车长(总路程) =(火车速度+人的速度)×迎面错过的时间;
(2)火车+同向行走的人:相当于追及问题
解法:火车车长(总路程) =(火车速度-人的速度) ×追及的时间;
(3)火车+坐在火车上的人:火车与人的相遇和追及问题
解法:火车车长(总路程) =(火车速度±人的速度) ×迎面错过的时间(追及的时间);
4、火车+火车:一个有长度、有速度,一个也有长度、有速度
(1)错车问题:相当于相遇问题
解法:快车车长+慢车车长(总路程) =(快车速度+慢车速度) ×错车时间;
(2)超车问题:相当于追及问题
解法:快车车长+慢车车长(总路程) =(快车速度-慢车速度) ×错车时间;
对于火车过桥、火车和人相遇、火车追及人以及火车和火车之间的相遇、追及等等这几种类型的题目,在分析题目的时候一定得结合着图来进行。
流水行船问题
理解了相对速度,流水行船问题也就不难了。
理解记住1个公式:顺水船速=静水船速+水流速度,就可以顺势理解和推导出其他公式:
逆水船速=静水船速-水流速度,
静水船速=(顺水船速+逆水船速)÷2,
水流速度=(顺水船速-逆水船 速)÷2。
技巧性结论如下:
1
相遇追及
水流速度对于相遇追及的时间没有影响,即对无论是同向还是相向的两船的速度差不构成“威胁”,大胆使用为善。
2
流水落物
漂流物速度=水流速度,t1= t2(t1:从落物到发现的时间段,t2:从发现到拾到的时间段)与船速、水速、顺行逆行无关。此结论所带来的时间等式常常非常容易的解决流水落物问题,其本身也非常容易记忆。
例题:
一条河上有甲、乙两个码头,甲码头在乙码头的上游50千米处。一艘客船和一艘货船分别从甲、乙两码头同时出发向上游行驶,两船的静水速度相同。
客船出发时有一物品从船上落入水中,10分钟后此物品距客船5千米。客船在行驶20千米后掉头追赶此物品,追上时恰好和货船相遇。求水流速度。
经典行程专题50道详解
1、甲、乙二人以均匀的速度分别从A、B两地同时出发,相向而行,他们第一次相遇地点离A地4千米,相遇后二人继续前进,走到对方出发点后立即返回,在距B地3千米处第二次相遇,求两次相遇地点之间的距离.
解答:第二次相遇两人总共走了3个全程,所以甲一个全程里走了4千米,三个全程里应该走4*3=12千米,通过画图,我们发现甲走了一个全程多了回来那一段,就是距B地的3千米,所以全程是12-3=9千米,所以两次相遇点相距9-(3+4)=2千米。
2、甲、乙、丙三人行路,甲每分钟走60米,乙每分钟走67.5米,丙每分钟走75米,甲乙从东镇去西镇,丙从西镇去东镇,三人同时出发,丙与乙相遇后,又经过2分钟与甲相遇,求东西两镇间的路程有多少米?
解:那2分钟是甲和丙相遇,所以距离是(60+75)×2=270米,这距离是乙丙相遇时间里甲乙的路程差,所以乙丙相遇时间=270÷(67.5-60)=36分钟,所以路程=36×(60+75)=4860米。
3、A,B两地相距540千米。甲、乙两车往返行驶于A,B两地之间,都是到达一地之后立即返回,乙车较甲车快。设两辆车同时从A地出发后第一次和第二次相遇都在途中P地。那么两车第三次相遇为止,乙车共走了多少千米?
解:根据总结:第一次相遇,甲乙总共走了2个全程,第二次相遇,甲乙总共走了4个全程,乙比甲快,相遇又在P点,所以可以根据总结和画图推出:从第一次相遇到第二次相遇,乙从第一个P点到第二个P点,路程正好是第一次的路程。所以假设一个全程为3份,第一次相遇甲走了2份乙走了4份。第二次相遇,乙正好走了1份到B地,又返回走了1份。这样根据总结:2个全程里乙走了(540÷3)×4=180×4=720千米,乙总共走了720×3=2160千米。
4、小明每天早晨6:50从家出发,7:20到校,老师要求他明天提早6分钟到校。如果小明明天早晨还是6:50从家出发,那么,每分钟必须比往常多走25米才能按老师的要求准时到校。问:小明家到学校多远?(第六届《小数报》数学竞赛初赛题第1题)
解:原来花时间是30分钟,后来提前6分钟,就是路上要花时间为24分钟。这时每分钟必须多走25米,所以总共多走了24×25=600米,而这和30分钟时间里,后6分钟走的路程是一样的,所以原来每分钟走600÷6=100米。总路程就是=100×30=3000米。
5、小张与小王分别从甲、乙两村同时出发,在两村之间往返行走(到达另一村后就马上返回),他们在离甲村3.5千米处第一次相遇,在离乙村2千米处第二次相遇.问他们两人第四次相遇的地点离乙村多远(相遇指迎面相遇)?
解:画示意图如下:
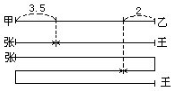
第二次相遇两人已共同走了甲、乙两村距离的3倍,因此张走了3.5×3=10.5(千米).
从图上可看出,第二次相遇处离乙村2千米.因此,甲、乙两村距离是10.5-2=8.5(千米).
每次要再相遇,两人就要共同再走甲、乙两村距离2倍的路程.第四次相遇时,两人已共同走了两村距离(3+2+2)倍的行程.其中张走了3.5×7=24.5(千米),24.5=8.5+8.5+7.5(千米).
就知道第四次相遇处,离乙村8.5-7.5=1(千米).答:第四次相遇地点离乙村1千米.
6、小王的步行速度是4.8千米/小时,小张的步行速度是5.4千米/小时,他们两人从甲地到乙地去.小李骑自行车的速度是10.8千米/小时,从乙地到甲地去.他们3人同时出发,在小张与小李相遇后5分钟,小王又与小李相遇.问:小李骑车从乙地到甲地需要多少时间?
解:画一张示意图:
图中A点是小张与小李相遇的地点,图中再设置一个B点,它是张、李两人相遇时小王到达的地点.5分钟后小王与小李相遇,也就是5分钟的时间,小王和小李共同走了B与A之间这段距离,它等于
这段距离也是出发后小张比小王多走的距离,小王与小张的速度差是(5.4-4.8)千米/小时.小张比小王多走这段距离,需要的时间是
1.3÷(5.4-4.8)×60=130(分钟).
这也是从出发到张、李相遇时已花费的时间.小李的速度10.8千米/小时是小张速度5.4千米/小时的2倍.因此小李从A到甲地需要
130÷2=65(分钟).
从乙地到甲地需要的时间是
130+65=195(分钟)=3小时15分.
答:小李从乙地到甲地需要3小时15分.
7、快车和慢车分别从A,B两地同时开出,相向而行.经过5小时两车相遇.已知慢车从B到A用了12.5小时,慢车到A停留半小时后返回.快车到B停留1小时后返回.问:两车从第一次相遇到再相遇共需多少时间?
解:画一张示意图:
设C点是第一次相遇处.慢车从B到C用了5小时,从C到A用了12.5-5=7.5(小时).我们把慢车半小时行程作为1个单位.B到C10个单位,C到A15个单位.慢车每小时走2个单位,快车每小时走3个单位.
有了上面“取单位”准备后,下面很易计算了.
慢车从C到A,再加停留半小时,共8小时.此时快车在何处呢?去掉它在B停留1小时.快车行驶7 小时,共行驶3×7=21(单位).从B到C再往前一个单位到D点.离A点15-1=14(单位).
现在慢车从A,快车从D,同时出发共同行走14单位,相遇所需时间是14÷(2+3)=2.8(小时).
慢车从C到A返回行驶至与快车相遇共用了7.5+0.5+2.8=10.8(小时).
答:从第一相遇到再相遇共需10小时48分.
9、一辆汽车从甲地开往乙地,如果车速提高20%,可以提前1小时到达。如果按原速行驶一段距离后,再将速度提高30%,也可以提前1小时到达,那么按原速行驶了全部路程的几分之几?
解:设原速度是1. 后来速度为1+20%=1.2
速度比值:
这是具体地反映:距离固定,时间与速度成反比.
时间比值 :6:5
这样可以把原来时间看成6份,后来就是5份,这样就节省1份,节省1个小时。
原来时间就是=1×6=6小时。
同样道理,车速提高30%,速度比值:1:(1+30%)=1:1.3
时间比值:1.3:1
这样也节省了0.3份,节省1小时,可以推出行驶一段时间后那段路程的原时间为1.3÷0.3=13/3
所以前后的时间比值为(6-13/3):13/3=5:13。所以总共行驶了全程的5/(5+13)=5/18
10、甲、乙两车分别从A,B两地出发,相向而行,出发时,甲、乙的速度比是 5:4,相遇后,甲的速度减少20%,乙的速度增加20%,这样,当甲到达B时,乙离A地还有10千米。那么A,B两地相距多少千米?
解:相遇后速度比值为[5×(1-20%)]:[4×(1+20%)]=5:6,假设全程为9份,甲走了5份,乙走了4份,之后速度发生变化,这样甲到达B地,甲又走了4份,根据速度变化后的比值,乙应该走了4×6÷5=24/5份,这样距A地还有5-24/5份,所以全程为10÷(1/5)×9=450千米。
11、A、B两地相距10000米,甲骑自行车,乙步行,同时从A地去B地。甲的速度是乙的4倍,途中甲的自行车发生故障,修车耽误了一段时间,这样乙到达占地时,甲离B地还有200米。甲修车的时间内,乙走了多少米?
解: 由甲共走了10000—200=9800(米),可推出在甲走的同时乙共走了9800÷4=2450(米),从而又可推出在甲修车的时间内乙走了10000—2450=7550(米)。列算式为10000一(10000—200)÷4=7550(米)
答:甲修车的时间内乙走了7550米。
12、爷爷坐汽车,小李骑自行车,沿一条公路同时从A地去B地。汽车每小时行40千米,是自行车速度的2.5倍。结果爷爷比小李提前3小时到达B地。A、B两地间的路程是多少千米?
解法一:根据“汽车的速度是自行车的2.5倍”可知,同时从A地到B地,骑自行车所花时间是汽车的2.5倍,也就是要比坐汽车多花1.5倍的时间,其对应的具体量是3小时,可知坐车要3÷(2.5一1)=2(小时),A、B两地问的路程为40×2=80(千米)。即40×〔3÷(2.5-1)〕80(千米)
解法二:汽车到B地时,自行车离B地(40÷2.5×3)=48(千米),这48千米就是自行车比汽车一共少走的路程,除以自行车每小时比汽车少走的路程,就可以得出汽车走完全程所用的时间,也就可以求出两地距离为40×〔(40÷2.5×3)÷(40-40÷2.5)〕=80(千米)
13、如图,有一个圆,两只小虫分别从直径的两端A与C同时出发,绕圆周相向而行。它们第一次相遇在离A点8厘米处的B点,第二次相遇在离c点处6厘米的D点,问,这个圆周的长是多少?
解: 如上图所示,第一次相遇,两只小虫共爬
行了半个圆周,其中从A点出发的小虫爬了8厘米,第二次相遇,两
只小虫从出发共爬行了1个半圆周,其中从A点出发的应爬行8×3=24(厘米),比半个圆周多6厘米,半个圆周长为8×3—6=18(厘米),一个圆周长就是:
(8×3—6)×2=36(厘米)
答:这个圆周的长是36厘米。
14、两辆汽车都从北京出发到某地,货车每小时行60千米,15小时可到达。客车每小时行50千米,如果客车想与货车同时到达某地,它要比货车提前开出几小时?
解法一:由于货车和客车的速度不同,而要走的路程相同,所以货车和客车走完全程所需的时间不同,客车比货车多消耗的时间就是它比货车提早开出的时间。列算式为
60×15÷50—15=3(小时)
解法二:①同时出发,货车到达某地时客车距离某地还有(60-50)×15=150(千米)
2客车要比货车提前开出的时间是:150÷50=3(小时)
17、甲、乙两人分别从A、B两地同时相向出发。相遇后,甲继续向B地走,乙马上返回,往B地走。甲从A地到达B地。 比乙返回B地迟0.5小时。已知甲的速度是乙的![]() 。甲从A地到达地B共用了多少小时?
。甲从A地到达地B共用了多少小时?
解:相遇时,甲、乙两人所用时间相同。甲从A地到达B地比乙返回B地迟0.5小时,即从相遇点到B地这同一段路程中,甲比乙多用0.5小时。可求出从相遇点到B地甲用了0.5÷(1一![]() )=2(小时),相遇时,把乙行的路程看做“l”,甲行的路程为
)=2(小时),相遇时,把乙行的路程看做“l”,甲行的路程为![]() ,从而可求
,从而可求
18、一个圆的周长为60厘米,三个点把这个圆圈分成三等分,3只甲虫A、B、C按顺时针方向分别在这三个点上,它们同时按逆时针方向沿着圆圈爬行,A的速度为每秒5厘米,B的速度为每秒1.5厘米,C的速度为每秒2.5厘米.问3只甲虫爬出多少时间后第一次到达同一位置?
解:我们先考虑B、C两只甲虫什么时候到达同一位置,C与B相差20厘米,C追上B需要20÷(2.5—1.5)=20(秒).而20秒后每次追及又需60÷(2.5-1.5)=60(秒);再考虑 A与C,它们第一次到达同一位置要20÷(5—2.5)=8(秒),而8秒后,每次追及又需60÷(5--2.5)=24(秒).可分别列出A与C、B与C相遇的时间,推导出3只甲虫相遇的时间
解:(1)C第一次追上B所需时间20÷(2.5—1.5)=20(秒).
(2)以后每次C追上B所需时间: 60÷(2.5—1.5)=60(秒).
(3)C追上B所需的秒数依次为: 20,80,140,200,….
(4)A第一次追上C所需时间:20÷(5—2.5)=8(秒).
(5)以后A每次追上C所需时间:60÷(5--2.5)=24(秒)
(6)A追上C所需的秒数依次为: 8,32,56,80,104….
19、甲、乙二人分别从A、B两地同时出发,如果两人同向而行,甲26分钟赶上乙;如果两人相向而行,6分钟可相遇,又已知乙每分钟行50米,求A、B两地的距离。
解: 先画图如下:
【方法一】 若设甲、乙二人相遇地点为C,甲追及乙的地点为D,则由题意可知甲从A到C用6分钟.而从A到D则用26分钟,因此,甲走C到D之间的路程时,所用时间应为:(26-6)=20(分)。
同时,由上图可知,C、D间的路程等于BC加BD.即等于乙在6分钟内所走的路程与在26分钟内所走的路程之和,为50×(26+6)=1600(米).所以,甲的速度为1600÷20=80(米/分),由此可求出A、B间的距离。
50×(26+6)÷(26-6)=50×32÷20=80(米/分)
(80+50)×6=130×6=780(米)
答:A、B间的距离为780米。
【方法二】设甲的速度是x米/分钟
那么有(x-50)×26=(x+50)×6
解得x=80
所以两地距离为(80+50)×6=780米
20.甲、乙两人同时从山脚开始爬山,到达山顶后就立即下山,他们两人的下山速度都是各自上山速度的1.5倍,而且甲比乙速度快,两人出发后1小时,甲与乙在离山顶600米处相遇,当乙到达山顶时,甲恰好下到半山腰。那么甲回到出发点共用多少小时?
解析:由甲、乙两人下山的速度是上山的1.5倍,有:
⑴甲、乙相遇时,甲下山600米路程所需时间,相当于甲上山走600÷1.5=400米的时间。所以甲、乙以上山的速度走一小时,甲比乙多走600+400=1000米。
⑵乙到山顶时,甲走到半山腰,也就是甲下山走了![]() 的路程。而走这
的路程。而走这![]() 路程所需时间,相当于甲上山走山坡长度
路程所需时间,相当于甲上山走山坡长度![]() ÷1.5=
÷1.5=![]() 的时间。所以在这段时间内,如
的时间。所以在这段时间内,如
保持上山的速度,乙走了一个山坡的长度,甲走了1+![]() =
=![]() 个山坡的长度。所以,甲上山的速度是乙的
个山坡的长度。所以,甲上山的速度是乙的![]() 倍。
倍。
用差倍问题求解甲的速度,甲每小时走:1000÷(![]() -1)×
-1)×![]() =4000米。
=4000米。
根据⑴的结论,甲以上山的速度走1小时的路程比山坡长度多400,所以山坡长3600米。
1小时后,甲已下坡600米,还有3600-600=3000米。所以,甲再用3000÷6000=0.5小时。
总上所述,甲一共用了1+0.5=1.5小时。
评注: 本题关键在转化,把下山的距离再转化为上山的距离,这种转化是在保证时间相等的情况下。通过转化,可以理清思路。但是也要分清哪些距离是上山走的,哪些是下山走的。
22.龟兔赛跑,全程5.2千米,兔子每小时跑20千米,乌龟每小时跑3千米,乌龟不停的跑;兔子边跑边玩,它先跑了1分钟后玩了15分钟,又跑了2分钟后玩15分钟,再跑3分钟后玩15分钟,......。那么先到达终点比后到达终点的快多少分钟?
解析:乌龟用时:5.2÷3×60=104分钟;兔子总共跑了:5.2÷20×60=15.6分钟。而我们有:15.6=1+2+3+4+5+0.6 按照题目条件,从上式中我们可以知道兔子一共休息了5次,共15×5=75分钟。所以兔子共用时:15.6+75=90.6分钟。 兔子先到达终点,比后到达终点的乌龟快:104-90.6=13.4分钟。
23.A、C两地相距2千米,C、B两地相距5千米。甲、乙两人同时从C地出发,甲向B地走,到达B地后立即返回;乙向A地走,到达A地后立即返回。如果甲速度是乙速度的1.5倍,那么在乙到达D地时,还未能与甲相遇,他们还相距0.5千米,这时甲距C地多少千米?
解析:由甲速是乙速的1.5倍的条件,可知甲路程是乙路程的1.5倍。设CD距离为x千米,则乙走的路程是(4+x)千米,甲路程为(4+x)×1.5千米或(5×2-x-0.5)千米。
列方程得: (4+x)×1.5=5×2-x-0.5
x=1.4 这时甲距C地:1.4+0.5=1.9千米。
24.张明和李军分别从甲、乙两地同时想向而行。张明平均每小时行5千米;而李军第一小时行1千米,第二小时行3千米,第三小时行5千米,……(连续奇数)。两人恰好在甲、乙两地的中点相遇。甲、乙两地相距多少千米?
解析:解答此题的关键是去相遇时间。由于两人在中点相遇,因此李军的平均速度也是5千米/小时。“5”就是几个连续奇数的中间数。因为5是1、3、5、7、9这五个连续奇数的中间数,所以,从出发到相遇经过了5个小时。甲、乙两地距离为5×5×2=50千米。
25.甲、乙、丙三人进行200米赛跑,当甲到达终点时,乙离终点还有20米,丙离终点还有25米,如果甲、乙、丙赛跑的速度都不变,那么当乙到达终点时,丙离终点还有多少米?
分析: 在相同的时间内,乙行了(200-20)=180(米),丙行了200-25=75(米),则丙的速度是乙的速度的175÷180=,那么,在乙走20米的时间内,丙只能走:20× 19![]() (米),因此,当乙到达终点时,丙离终点还有25-19
(米),因此,当乙到达终点时,丙离终点还有25-19![]() =5(米)。
=5(米)。
解:25-20×=25-20=25-19![]() =5
=5![]() (米)。
(米)。
26.老师教同学们做游戏:在一个周长为114米的圆形跑道上,两个同学从一条直径的两端同时出发沿圆周开始跑,1秒钟后他们都调头跑,再过3秒他们又调头跑,依次照1、3、5……分别都调头而跑,每秒两人分别跑5.5米和3.5米,那么经过几秒,他们初次相遇?
解析:⑴半圆周长为144÷2=72(米)先不考虑往返,两人相遇时间为:72÷(5.5+3.5)=8(秒)
⑵初次相遇所需时间为:1+3+5+……+15=64(秒)。
27.甲、乙两地间有一条公路,王明从甲地骑自行车前往乙地,同时有一辆客车从乙地开往甲地。40分钟后王明与客车在途中相遇,客车到达甲地后立即折回乙地,在第一次相遇后又经过10分钟客车在途中追上了王明。客车到达乙地后又折回甲地,这样一直下去。当王明骑车到达乙地时,客车一共追上(指客车和王明同向)王明几次?
解析:设王明10分钟所走的路程为a米,则王明40分钟所走的路程为4a米,则客车在10分钟所走的路程为4a×2+a=9a米,客车的速度是王明速度的9a÷a=9倍。
王明走一个甲、乙全程则客车走9个甲、乙全程,其中5个为乙到甲地方向,4个为甲到乙地方向,即客车一共追上王明4次。
28.迪斯尼乐园里冒失的米老鼠和唐老鸭把火车面对面的开上了同一条铁轨,米老鼠的速度为每秒10米,唐老鸭的速度为每秒8米。由于没有及时刹车,结果两列火车相撞。假如米老鼠和唐老鸭在相撞前多少秒同时紧急刹车,不仅可以避免两车相撞,两车车头还能保持3米的距离。(紧急刹车后米老鼠和唐老鸭的小火车分别向前滑行30米)。
答案:(30×2+3)÷(10+8)=3.5秒。
29.A、B是一圈形道路的一条直径的两个端点,现有甲、乙两人分别从A、B两点同时沿相反方向绕道匀速跑步(甲、乙两人的速度未必相同),假设当乙跑完100米时,甲、乙两人第一次相遇,当甲差60米跑完一圈时,甲、乙两人第二次相遇,那么当甲、乙两人第十二次相遇时,甲跑完几圈又几米?
解析:甲、乙第一次相遇时共跑0.5圈,乙跑了100米;第二次相遇时,甲、乙共跑1.5圈,则乙跑了100×3=300米,此时甲差60米跑一圈,则可得0.5圈是300-60=240米,一圈是480米。 第一次相遇时甲跑了240-100=140米,以后每次相遇甲又跑了140×2=280米,所以第十二次相遇时甲共跑了:140+280×11=3220=6圈340米。
30.甲、乙两人步行的速度之比是7:5,甲、乙分别由A、B两地同时出发。如果相向而行,0.5小时后相遇;如果他们同向而行,那么甲追上乙需要多少小时?
解析:(1)设甲追上乙要x小时。
因为相向而行时,两人的距离÷两人的速度和=0.5小时,同向而行时,两人的距离÷两人的速度差=x小时。 甲、乙两人的速度之比是7:5,所以
(2)根据路程之比等于速度之比可知,相遇时甲行7份,乙行5份(总路程12份),0.5小时内甲比乙多行7-5=2份。追及时甲要追上乙,需要多行12份,即12÷2×0.5=3小时。
31.甲、乙两人分别从A、B两地同时出发,相向而行,出发时他们的速度之比是3:2,他们第一次相遇后甲的速度提高了20﹪,乙的速度提高了30﹪,这样,当甲到达B地时,乙离A地还有14千米,那么A、B两地的距离是多少千米?
解析:因为他们第一次相遇时所行的时间相同,所以第一次相遇时甲、乙两人行的路程之比也为3:2相遇后,甲、乙两人的速度比为〔3×(1+20﹪)〕:〔2×(1+30﹪)〕=3.6:2.6= 18:13到达B地时,即甲又行了2份的路程,这时乙行的路程和甲行的路程比是18:13,即乙的路程为2×=1![]() 。乙从相遇后到达A还要行3份的路程,还剩下3-1
。乙从相遇后到达A还要行3份的路程,还剩下3-1![]() =1
=1![]() (份),正好还剩下14千米,所以1份这样的路程是14÷1
(份),正好还剩下14千米,所以1份这样的路程是14÷1![]() =9(千米)。A、B两地有这样的3+2=5(份),因此A、B两地的总路程为:
=9(千米)。A、B两地有这样的3+2=5(份),因此A、B两地的总路程为:
[3×(1+20%)]:[2×(1+30%)]=18:13
14÷(3-2×)=14÷1![]() =9(千米)
=9(千米)
9×(3+2)=45(千米)
答:A、B两地的距离是45千米。
32.一条船往返于甲、乙两港之间,已知船在静水中的速度为每小时9千米,平时逆行与顺行所用的时间比为2:1。一天因为下暴雨,水流速度是原来的2倍,这条船往返共用了10小时,甲、乙两港相距多少千米?
解析: 平时逆行与顺行所用的时间比为2:1,设水流的速度为x,则9+x=2(9-x),x=3。那么下暴雨时,水流的速度是3×2=6(千米),顺水速度就是9+6=15(千米),逆水速度就是9-6=3(千米)。逆行与顺行的速度比是15:3=5:1。逆行用的时间就是10×=(小时),两港之间的距离是3×=25(千米)。
33.姐弟俩正要从公园门口沿马路向东去某地,他们回家要从公园门口沿马路向西行,他们商量是先回家取车再骑车去某地省时间,还是直接从公园门口步行向东去某地省时间。姐姐算了一下:已知骑车与步行的速度之比是4︰1,从公园门口到达某地距离超过2千米时,回家取车才合算。那么,公园门口到他们家的距离有多少米?
解析:从题中“公园门口到达某地距离超过2千米时,回家取车才合算”,可以知道,从公园门口到某地距离是2千米时,则两者时间相同。设公园门口到家的距离是x千米。
8-4x=x+2
x=1.2
答:从公园门口到他们家的距离有1.2米。
34.猎犬发现在离它10米远的前方有一只奔跑着的野兔,马上紧追上去,猎犬的步子大,它跑5步的路程,兔子要跑9步,但是兔子的动作快,猎犬跑2步的时间,兔子却要跑3步。猎犬至少跑多少米才能追上兔子?
解析:此题是追及问题,需要根据求出追及时间t.
由“它跑5步的路程,兔子要跑9步”可得相同路程步数的比为5:9;由“猎犬跑2步的时间,兔子却要跑3步”可得相同时间步数的比为2:3=6:9。把“兔子跑9步”的距离作为单位1,同一时间内猎犬跑单位1的![]() 。时间一定则速度与路程成正比,所以猎犬与兔子的速度比为6:5,即速度差为(1-
。时间一定则速度与路程成正比,所以猎犬与兔子的速度比为6:5,即速度差为(1-![]() )=
)=![]() ,因此猎犬至少跑10÷
,因此猎犬至少跑10÷![]() =60米才能追上兔子。
=60米才能追上兔子。
36、甲、乙二人同时从A地去280千米外的B地,两人同时出发,甲先乘车到达某一地点后改为步行,车沿原路返回接乙,结果两人同时到达B地。已知甲、乙二人步行的速度是5千米/小时,汽车的速度是每小时55千米。问甲下车的地点距B还有多少千米?
【分析】:甲、乙二人走的路程均分为步行、乘车两部分,两人速度相等,这说明,二人乘车的路程和步行的路程分别相等.由于二人步行的速度为每小时5千米,乘车的速度为每小时55千米,所以,在相同的时间里,乘车所走的路程是步行所走路程的11倍.
【解】:注意到乘车速度是人的11倍,那么相同时间下走的距离也是步行的11倍
由于甲乙同时到达因此两人步行的距离相同,把这个距离看做1份
可以设甲在c下车,车回去在d接上了乙
因此AD=BC AC+CD=11AD=11份,所以2AC=12份。故AC是6份 全长AB就是7份=280千米
所以一份是40千米
37、如图所示,沿着某单位围墙外面的小路形成一个边长300米的正方形,甲、乙两人分别从两个对角处沿逆时针方向同时出发。已知甲每分走90米,乙每分走70米。问:至少经过多长时间甲才能看到乙?
【解答】当甲、乙在同一条边(包括端点)上时甲才能看到乙。甲追上乙一条边,即追上300米需300÷(90-70)=15(分),此时甲、乙的距离是一条边长,而甲走了90×15÷300=4.5(条边),位于某条边的中点,乙位于另一条边的中点,所以甲、乙不在同一条边上,甲看不到乙。甲再走0.5条边就可以看到乙了,即甲总共走了5条边后就可以看到乙了,共需要小时。
38、某列车通过250米长的隧道用25秒,通过210米长的隧道用23秒,若该列车与另一列长150米.时速为72千米的列车相遇,错车而过需要几秒钟?
解:根据另一个列车每小时走72千米,所以,它的速度为:72000÷3600=20(米/秒),
某列车的速度为:(25O-210)÷(25-23)=40÷2=20(米/秒)
某列车的车长为:20×25-250=500-250=250(米),
两列车的错车时间为:(250+150)÷(20+20)=400÷40=10(秒).
39、甲、乙之间的水路是234千米,一只船从甲港到乙港需9小时,从乙港返回甲港需13小时,问船速和水速各为每小时多少千米?
答案: 从甲到乙顺水速度:234÷9=26(千米/小时)。
从乙到甲逆水速度:234÷13=18(千米/小时)。
船速是:(26+18)÷2=22(千米/小时)。
水速是:(26-18)÷2=4(千米/小时)。
41、甲、乙两港相距360千米,一轮船往返两港需35小时,逆流航行比顺流航行多花了5小时。现在有一机帆船,静水中速度是每小时12千米,这机帆船往返两港要多少小时?
分析与解:要求帆船往返两港的时间,就要先求出水速。由题意可以知道,轮船逆流航行与顺流航行的时间和与时间差分别是35小时与5小时,用和差问题解法可以求出逆流航行和顺流航行的时间.并能进一步求出轮船的逆流速度和顺流速度。在此基础上再用和差问题解法求出水速。
解:轮船逆流航行的时间:(35+5)÷2=20(小时),顺流航行的时间:(35-5)÷2=15(小时),轮船逆流速度:360÷20=18(千米/小时),顺流速度:360÷15=24(千米/小时),
水速:(24—18)÷2=3(千米/小时),帆船的顺流速度:12+3=15(千米/小时),
帆船的逆水速度:12—3=9(千米/小时),帆船往返两港所用时间:
360÷15+360÷9=24+40=64(小时)。
答:机帆船往返两港要64小时。
42、 某船往返于相距180千米的两港之间,顺水而下需用10小时,逆水而上需用15小时。由于暴雨后水速增加,该船顺水而行只需9小时,那么逆水而行需要几小时?
分析与解:本题中船在顺水、逆水、静水中的速度以及水流的速度都可以求出。但是由于暴雨的影响,水速发生变化,要求船逆水而行要几小时,必须要先求出水速增加后的逆水速度。
解:船在静水中的速度是:(180÷10+180÷15)÷2=15(千米/小时)。
暴雨前水流的速度是:(180÷10-180÷15)÷2=3(千米/小时)。
暴雨后水流的速度是:180÷9-15=5(千米/小时)。
暴雨后船逆水而上需用的时间为:180÷(15-5)=18(小时)。
答:逆水而上需要18小时。
43、一条隧道长360米,某列火车从车头入洞到全车进洞用了8秒钟,从车头入洞到全车出洞共用了20秒钟。这列火车长多少米?
分析与解:画出示意图
如图 :火车8秒钟行的路程是火车的全长,20秒钟行的路程是隧道长加火车长。因此,火车行隧道长(360米)所用的时间是(20-8)秒钟,即可求出火车的速度。
解火车的速度是360÷(20-8)=30(米/秒)。
火车长30×8=240(米)。
答:这列火车长240米
44、铁路旁的一条与铁路平行的小路上,有一行人与骑车人同时向南行进,行人速度为3.6千米/时,骑车人速度为10.8千米/时,这时有一列火车从他们背后开过来,火车通过行人用22秒,通过骑车人用26秒,这列火车的车身总长是多少?
【解】:分析:本题属于追及问题,行人的速度为3.6千米/时=1米/秒,骑车人的速度为10.8千米/时=3米/秒。火车的车身长度既等于火车车尾与行人的路程差,也等于火车车尾与骑车人的路程差。如果设火车的速度为x米/秒,那么火车的车身长度可表示为(x-1)×22或(x-3)×26,由此不难列出方程。
法一:设这列火车的速度是x米/秒,依题意列方程,得
(x-1)×22=(x-3)×26。
解得x=14。所以火车的车身长为 (14-1)×22=286(米)。
法二:直接设火车的车长是x, 那么等量关系就在于火车的速度上。
可得:x/26+3=x/22+1
这样直接也可以x=286米
法三:既然是路程相同我们同样可以利用速度和时间成反比来解决。
两次的追及时间比是:22:26=11:13
所以可得:(V车-1):(V车-3)=13:11
可得V车=14米/秒
所以火车的车长是(14-1)×22=286(米)
答:这列火车的车身总长为286米。
45、一条单线铁路上顺次有A、B、C、D、E五个车站,它们之间的距离依次是48、40、10、70千米。甲、乙两列火车分别从A、E两站相对开出,甲车先开4分钟,每小时行驶60千米,乙车每小时行驶50千米。两车只能在车站停车,互相让道错车。两车应在哪一车站会车(相遇),才能使停车等候的时间最短?先到的火车至少要停车多少时间?
【解答】 A、E两站相距千米,甲先开4分钟,行驶了千米,若不考虑靠站错车,两列火车经过小时相遇,相遇地点距离E点千米,恰在C、D段的重点处,则可以考虑让甲车在C处等候或乙车在D处等候。
若让甲车在C处等候,等候时间为小时;
若让乙车在D处等候,等候时间为小时。
比较可知,两车应在D处会车,先导的火车至少要停车![]() 小时,即10分钟。
小时,即10分钟。
46、 乙船顺水航行2小时,行了120千米,返回原地用了4小时.甲船顺水航行同一段水路,用了3小时.甲船返回原地比去时多用了几小时?
分析与解:乙船顺水速度:120÷2=60(千米/小时).乙船逆水速度:120÷4=30(千米/小时)。
水流速度:(60-30)÷2=15(千米/小时).甲船顺水速度:12O÷3=4O(千米/小时)。
甲船逆水速度:40-2×15=10(千米/小时).甲船逆水航行时间:120÷10=12(小时)。
甲船返回原地比去时多用时间:12-3=9(小时)。
47、现在是3点,什么时候时针与分针第一次重合?
分析与解:3点时分针指12,时针指3。分针在时针后5×3=15(个)格.
48、有一座时钟现在显示10时整。那么,经过多少分钟,分针与时针第一次重合;再经过多少分钟,分针与时针第二次重合?
解:10时整,分针与时针距离是10格,需要追击的距离是(60-10)格,分针走60格,时针走5格,即分针走1格,时针走5/60=1/12格。
第一次重合经过 (60-10)/(1-1/12)=54(6/11)(分)
第二次重合再经过 60/(1-1/12)=65(5/11)(分)
答:经过54(6/11)分钟,分针与时针第一次重合;再经过65(5/11)分钟,分针与时针第二次重合。
2点钟以后,什么时刻分针与时针第一次成直角?
分析与解:在2点整时,分针落后时针5×2=10(个)格,当分针与时针第一次成直角时,分针超过时针60×(90÷360)=15(个)格,因此在这段时间内分针要比时针多走10+15=25(个)格,所以到达这一时刻所用的时间为:
49、在9点与10点之间的什么时刻,分针与时针在一条直线上?
分析与解:分两种情况进行讨论。①分针与时针的夹角为180°角:
当分针与时针的夹角为180°角时,分针落后时针60×(180÷360)=30(个)格,而在9点整时,分针落后时针5×9=45(个)格.因此,在这段时间内分针要比时针多走45-30=15(个)格,而每分钟分针比时针多走
(分钟)。
②分针与时针的夹角为0°,即分针与时针重合:
9点整时,分针落后时针5×9=45(个)格,而当分针与时针重合时,分针要比时针多走45个格,因此到达这一时刻所用的时间为:45÷(1-1/12)=49又1/11(分钟)
50、晚上8点刚过,不一会小华开始做作业,一看钟,时针与分针正好成一条直线。做完作业再看钟,还不到9点,而且分针与时针恰好重合。小华做作业用了多长时间?
分析与解:这是一个钟面上的追及问题。分针每分钟走1格,时针每分钟走1/12格,相差(1-1/12)格(速度差)。分针与时针成一条直线,是说分针与时针相隔30格(追及路程),两针重合是说分针追上了时针。解略。答案:32又8/11(分钟)
Copyright © 2019 百思威科技版权所有
